The first part of this series of posts was about waveforms - and the 30dB rule applies to both analogue or digital waveforms (although a high resolution LCD might get you to 40dB!). The second part was the same - all of the terminology applies to any way of storing the waveform. This part looks at digital storage of single cycle waveforms.
[As an aside: There have been several synthesizers with analogue oscillators that provided 'waveform drawing' controls (and I designed and built one of my own many decades ago), but they tend to use very small numbers of points to represent the waveform. I have always had a design rule of not having more than 8 sliders in a group on a synthesizer - and in fact, the 'rule of 5' probably over-rides that. (Once you get beyond five user controls closely packed together, then people find it harder and harder to locate a specific control... Take a look at modern synth UI designs, and you will see 'Rule of 5' everywhere...) So 16 (or more) sliders is cumbersome, expensive, slow to adjust, suffers badly from 'The 30dB Rule', and isn't enough points to get good waveforms when compared to a single rotary 'preset waveform' selection switch! (It also looks too much like a third octave graphic equaliser!) In these days where 'vintage' and 'analogue' seem to have huge customer appeal, then I wouldn't be at all surprised to see a synth with lots of sliders to set a waveform, maybe doubling up as additive synthesis controls.]
WAVs
One of the common ways to use digital single cycle waveforms is via .WAV files. WAVs are tagged file format files that are used to store and exchange digital audio, and are examples of a RIFF file (Resource Interchange File Format) which was defined by IBM and Microsoft (and is the native audio file format in Microsoft Windows (and is actually closely related to the AIFF files that you find on Apple products as well...) WAV is actually shorthand for Waveform Audio File Format, which ought to mean that it should be WAFF (I can't help imagining an alternative universe where table tennis is colloquially called Wiff-Waff instead of Ping-Pong, and where WAAF files have nothing to do with the Women's Auxiliary Air Force from WW2...). There's plenty of detail on
the WAV file format on Wikipedia (Disclosure: I'm a donator to Wikipedia.)
Aside from all this tech-talk, WAV files are in very widespread use for exchanging uncompressed audio between computers and sample players, grooveboxes, other computers, drum machines, etc. Note that although WAVs can contain compressed audio, you are much more likely to find compressed audio in a format that builds on MP3, like AAC, but it is quite rare to find any support for this in drum machines, grooveboxes etc. The 'higher-end' BWF multi-channel version is widely used in the broadcast and pro-audio industry, but again has limited support in drum machines, grooveboxes, etc. But at the opposite end of things, WAVs are very often used for storing and transferring single cycle waveforms, and support for WAVs is pretty close to obligatory in a groovebox, drum machine... As always, there's bound to be some exceptions so that people can look smart by saying: 'Ah, but'.
A Google search for 'single cycle waveforms' will probably get you lots of references to the Adventure Kid web-site and the Elektron 'Elektronauts' forum site (both recommended for getting single cycle waveforms), plus many commercial offerings. As with various projects to create all possible MIDI melodies, various people have tried to exhaustively create all possible single cycle waveforms within specific limitations, although the copyright and other legal systems seem to not like any type of mechanistic/algorithmic brute-force approach that intends to try and acquire ownership of creative activities.
The obvious...
As you might expect, the first single cycle waveforms you will find are probably going to be the 'classic' synthesizer waveforms: sine, triangle, square, sawtooth, and various pulse widths. I'm going to show them here for reference, complete with their harmonic content or spectra (spectrums, if you prefer), although, as the next blog post shows, just having the spectrum for a waveform may not be as useful as you might think. For now, I will just describe what the spectra shows about the basic harmonic content of the waveshape, and you will be forewarned that there is just a little bit more to it...
One of the first things that people tend to do with digital storage of audio is to turn classic analogue synthesizer waveforms into a digital form, so let's start there...
Sine
The sine is a beautifully smooth and curvy looking, simple and pure sounding waveform. It contains (it is!) just a single frequency (called the fundamental, and 100Hz in this example), and so has no harmonics in it. (multiples of the fundamental frequency) For LFOs, sine waves are very useful because they smoothly modulate, or pan, or filter, or...
However, using only a few samples to represent the waveform isn't a good way to get the best fidelity. I have seen single cycle waveforms of sine waves that only have 37 samples. Which takes us neatly into why particular numbers of samples are used for single cycle waveforms.
There is a lot of variation in the numbers of samples that are used to represent a single cycle waveform. In Max (and MaxForLive), the ~cycle object originally defaulted to using 512 samples of a single cycle of a cosine wave. But it wasn't fixed - you could replace the default waveform by using any other set of 512 samples, or you could change the number of samples: more recent versions of Max use 16,000 64-bit samples. A lot of the single cycle waveforms that you find on the InterWeb are 337 samples long, whilst others have 256, 1024, 2048 or 4096.
You may be confused by these numbers, but remember that these are not sample rates: like 44.1kHz, 48kHz, or 96kHz. These big numbers are the rate at which samples are taken. If a mono audio signal is recorded for 1 second at 44.1kHz, then there will be 44,100 samples that represent that one second of audio. One Hertz is one cycle per second, and so if that one second contained a 1Hz sine wave, then there would be 44,100 samples being used to represent that sine wave. 10Hz would be 10 cycles in one second, and so a single cycle of a 10Hz sine wave would only require 4,410 samples. 100Hz would be 441 samples, which is pretty close to the 512 that Max used to have as the default. However, 1,000Hz would require 44.1 samples, which is tricky. It is a small number (just above 37!), and it isn't a whole number of samples... What does 0.1 of a sample look like, or is it just impossible?
Rather than get involved in strange philosophical questions about fractions of samples, it is easier to arrange things so that a single cycle waveform is exactly the right frequency to fill a given number of samples with one complete cycle. No more. No less. In the case of the 100Hz sine wave, sampled at 44.1kHz, we now know that 441 samples is exactly the right length. (Or we could say that 441 samples will hold a single cycle of a 100Hz sine wave when the sampling rate is 44.1kHz.) Unfortunately, 441 isn't 512, or 337, or 4096, or 16,000!
What we need to do is turn this round, so that we can work out the frequency of the waveform that will fill a given number of samples for a specific sample rate (like 44.1kHz!). If we take 512 as an example, then the frequency of a single cycle that will fill 512 samples is 86.1328125. Now frequencies that are not whole numbers are fine - so we avoid any problems with 0.1 of a sample! But how did we work that out?
If you divide the sample rate (44,100) by the number of samples (512) that you want to use in your single cycle waveform, and you get exactly 86.1328125. But it is actually easier to understand what is happening here by turning the equation over. In other words, what does 512 divided by 44,100 represent? Well, the number of samples divided by rate that samples are being taken is going to give us what fraction 512 is of 44,100. It turns out that this is 0.01158371. So 512 is just over one hundredth part of 44,100. In fact, if you think about it, then 441 would be exactly one hundredth of 44,100. So what does the fraction represent? It is samples (512) over the sample rate (44,100) and so it is just 1/rate. And to get to the rate (which is the frequency) then all we need to do is find the value of 1 divided by the fraction. 1/0.01158371 is 86.1328125, which is the rate that we need to use to fill that fraction of 512/44,1000.
So the formula is:
Frequency for a single cycle = Sample Rate / Number of samples for one cycle
Using this, we can now look at some of those common numbers of samples and see what frequency they give for a 44.1kHz sampling rate:
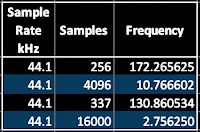 |
Table 1. Sample Rate, Number of Samples and Required Frequency. |
At this point, many people look at the numbers, with all the digits after the decimal point, and just accept them. But it turns out that the 'Popular on the InterWeb' value, 337, gives a frequency which might be familiar... Maybe doubling it will help? 261.721068?
What is the frequency of Middle C? 261.625565Hz. Aha! 337 is chosen because it is very close to Middle C, and so simplifies the transposition of oscillators using 337 sample waveforms (i.e., you don't need to transpose them!). It turns out that a lot of the single cycle waveforms that you find on the internet have a frequency of one octave below Middle C.
Triangle
This is kind of like a sine wave drawn by someone who prefers straight lines to curves. It contains only a few odd harmonics that are are quite low amplitudes - so with a fundamental at 172.265625Hz, the 3x harmonic is at -25dB, and is at 516.796875Hz. What is fascinating about generating and analysing real waveforms instead of the ones that you find in text-books is that they can be very different because of all sorts of imperfections in the generation, capture and analysis processes. 600 samples is not going to give perfect results for a start...
I'm not really a triangle waveform fan. Triangle waves are not very useful because a little bit of low-pass filtering reveals the sine wave at their core, and opening up the low pass filter only adds a little bit of extra harmonic content. For LFOs, triangle waves spend almost all their time linearly going up or down, but then suddenly (and very abruptly) change direction. So whereas a sine wave is all about smoothly getting to the point where it reverses direction, a triangle wave rather boringly goes straight to the point, immediately changes direction, and then goes straight towards the next reversal. A bit too jerky in many cases for me, and I often prefer the smooth almost asymptotic sine wave. (Asymptotic means that it never quite gets there...)
Square
The square wave, despite what the shape might suggest, is actually exactly the same harmonics as the triangle waveform, but with slightly higher amplitudes. As you can see, the 3x harmonic of the 73.5Hz fundamental, at 220.5Hz, is only at about -10dB, and then the 4x harmonic (which isn't odd, and shouldn't be there) is at 294Hz and is at about -15dB. For the full story, you are just going to have to see the next blog post... For LFOs, then the square couldn't be more different than the triangle or the sine wave - it stays at the same level for half the time, then suddenly jumps to the other level, and then stays there for the other half of the time, then jumps again.
Sawtooth
There are two ways of showing a sawtooth. The one shown here starts at the gently sloped zero crossing and goes up, then suddenly plummets down, and then rises again. The other way starts with the zero crossing on the steep sloe, then has a single long upwards slope, finishing with the sudden downwards plunge. Unlike all of the waveforms so far, there are two different sawtooth waveforms: one where the gentle slope is upwards (a rising sawtooth, or a saw up) and another where the gentle slope is downwards (a falling sawtooth or a saw down). Showing the rising sawtooth like this kind of follows the other waveforms nicely. This time, the harmonics are the expected ones: odd and even harmonics gradually dropping off in amplitude.
For LFOs, then the two sawtooth waveforms can have very different effects: a rising sawtooth used for pitch modulation gives rising frequencies, for example, whilst a falling sawtooth would give descending frequencies. On modulars, I have always been a fan of using a sawtooth and its inversion (if you invert a falling sawtooth it becomes a rising sawtooth (and vice-versa)!) for controlling things in opposite ways.
At audio frequencies, then Up/Rising and Down/Falling sawtooth waveforms sound exactly the same, and they have the same harmonics at the same levels.
If the sine wave is the ultimate in smoothness, and the square wave the ultimate in jerkiness, the sawtooth is pretty much the exact opposite of smooth - as a control and as a timbre.
Pulse
There are lots of pulse waveforms - anything that just jumps between the upper and lower limits that doesn't split the time 50:50 is, by definition, a pulse waveform. Some people say that a square wave is nothing more than a special case of a pulse. Many oscillators aren't very happy doing very short pulse widths, and so I won't be doing 1% or 99% waveforms here (again, like sawtooths, you have two opposite wave shapes, but not as good looking! And again, pulse waveforms with the same time split sound the same...).
Pulse waveforms are described in various ways: as ratios (1:1 is a square wave), as percentages (50% is a square wave) , and sometimes the ratio/percentage is called a duty cycle, which is an obscuring piece of jargon that seems to be used less and less.
First, something like a 22% pulse waveform:
The big blob on the left hand side is the DC offset, by the way. Pulse waveforms have them because they are not symmetrical around the zero axis. (The area under the positive part of the waveform is not the same as the area bounded by the negative part of the waveform - which is why the square waveform is 'special': it has no DC offset!) But the harmonics are high in amplitude: the fundamental at 73.5Hz is at -2dB, and the 2x harmonic is only at -6dB, and there are lots of other harmonics that are above the -40dB 'Rule' level, so they definitely will be visible on a waveform display!
In an LFO, then pulse waves are kind of like square wave, but the different time that is spent at the two levels is not to my taste. Once again, like sawtooths, there are two varieties of pulse: each the inverse of the other, and all just as boring.
For a 10% pulse, then it is just more:
The DC offset is really big now! But look at how the harmonics are very high as well. Compare this with the triangle and square wave to see the differences.
As was mentioned in part 2 of this series, the more jagged the waveform, the more high frequencies that will be present. A 10% pulse waveform is pretty jagged, in shape and in sound, and the spectrum contains lots of harmonics at high amplitudes.
In an LFO, a 10% pulse waveform is boring for 90% of the time, then jumps to the other level for 10% of the time, and then is boring again. Not my favourite LFO control waveform. If a sine waveform can be described as being 'smooth' in sound and effect, and a sawtooth waveform is 'jerky', then a pulse waveform is 'boring - except for a very short amount of time'. There is an exception to this, and it is found in a lot of advanced modular setups: if you combine several LFOs with pulse waveforms, then you start to get a control which is good for random percussive or rhythmic sounds, sort of like digital LFO 'noise'. Curiously, having a 'noise-like' 'random-ish' 'difficult to predict' control like this often sounds more interesting that proper random noise, perhaps because human beings are preprogrammed to look for/listen for/find/feel patterns.
Beyond the obvious...
There are more waveforms!
If you add a sawtooth and a square wave together, then you get a sort of droopy waveform.
This is a strange waveform, so I have shown more than one cycle of it so that you get a better feel of what it looks like. The spectrum, as you might expect, has elements of the sawtooth and the square spectra.
In an LFO, this is like a jerky rising or falling sawtooth. It doesn't have the inevitability of the inexorably rising (or falling) sawtooth, or the boring static levels of the square, but it does have the sudden jumps of both. I'm not sure that I've ever used this wave shape in an LFO...
Hyper!
If you replace the linear slope of a sawtooth with a curve, then you get a hypersawtooth waveform, although this term is also sometimes used for several sawtooth oscillators summed together.
Once again, I have shown several cycles so that you get a clearer view of the shape. It's a sawtooth where the linear slope is replaced with two curves - and the shape of those curves determines the fine detail of the spectrum. For the first time, the fundamental is not the highest frequency in the spectrum - the 2x harmonic is higher! What this means is that there are lots of high frequencies in a hypersawtooth, and so it sounds brighter than a sawtooth or a narrow pulse.
In LFOs, the hypersaw shape is a bit like a sine with a wobble in the middle. I have not used it very much.
Transpositions...
Something else which is 'non obvious' is working out what the required transposition should be for those single cycle waveforms that aren't 337 samples long. This seems to give people problems, but all it requires is to convert the ratio of the two frequencies to semitones and cents. Here's a table that extends the previous one:
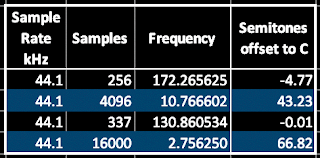 |
Table 1. Sample Rate, Number of Samples, Required Frequency, and Required Transposition.
|
So for a 256 sample single cycle waveform, you just transpose it down by 4 semitones and 77 cents.
From the classics...
One type of single cycle waveform that you probably find are based on the shapes of 'classic' analogue synthesizers - not the mathematically perfect waveforms that you find in text-books. The '30dB Rule' probably applies here, plus there is also the assumption that vintage analogue synths repeat exactly the same waveform every cycle. Then there is the problem that a lot of the character and 'sound' of many synthesizers is dynamic: the way that filters distort, or the way that filters go into self-oscillation, DC offsets affecting clipping in output stages, or the way that the oscillator sound bleeds between oscillators, and lots more. Timbre is more than just a static sound, it is how the sound changes over time and under the influence of performance controls like the Pitch Bend Wheel, the Mod Wheel, After-touch, etc., as well as the interactions between various parts of the device itself (beehive noise, for example), and trying to capture this in a single cycle waveform is not always easy.
You may well find some 'single cycle waveforms from classic synths' that you like, but don't forget to add a bit of noise into the audio, into the filter cut-off and resonance, detune the oscillators, add a bit of chorus and basically 'productionise' it as if it was a real old synth that costs a fortune to maintain and which spends part of each year being serviced. Who knows, you might find that the contribution from the single cycle waveform is not as important as some of the other post-processing...
Not what you expected!
One of the fascinating things about single cycle waveforms is when they catch you out. One standard example is creating a single cycle waveform using noise, so that you get a 'random' wave shape. A lot of people expect that this will create white noise, and are disappointed when they get a buzzy tone. Unfortunately, because each cycle of the waveform derived from random noise repeats every cycle, you get a tone instead of noise. Depending on the source of the noise and how it is captured, then there may well be lots of high frequencies - In general, the more jagged the waveform, the more high frequencies that are produced. So single cycle waveforms made from noise almost always end up giving very thin, bright, nasal, buzzy results.
In contrast, two programming techniques that can produce excellent results from singe cycle waveforms are Oscillator Sync and FM. The sound of sawtooth wave or square wave sync is very well-known, but if you use two different, unusual single cycle waveforms instead, then you can get some more unusual and distinctive timbres. For FM, then avoid the obvious sine waves, and explore shapes like triangle waves, or sawtooths or filtered noise waveforms (yep, you just knew that those noise waveforms had to be useful somewhere!). FM has an interesting reputation (and there are lots of YouTube videos that try to put you more at ease), and who knows, you may stumble into some of the less-explored backwaters of Chowning's wobbly oceans and find some gems.
No room for innovation...
So is there any space left for new or novel or unusual singe cycle waveforms? I'm going to share some of my own attempts to be different. Some of them are not very special, but I'm hoping that some of them might be useful to you.
Sine and Square...
The first 'off the wall' approach is to mix waveforms that normally don't go together. How about a cycle of sine wave followed by a cycle of square wave? Technically, this is a multi cycle waveform, but most oscillators don't care, and you will find that you have a lower frequency in the resulting sound because the square wave is effectively only present half the time, and so you get something a bit like a weird sub oscillator, plus something that isn't a sine or a square. Once again I have included a little bit more after the end of the cycle, so that you can see the repeat - yes, the 'single cycle' is the sine wave cycle plus the square wave cycle!
The spectrum tells us a lot about what this is going to sound like, there's a slightly lower fundamental and a big 2x harmonic frequency, and then strong clusters of higher frequencies. Despite being just two cycles of very simple wave shapes, this is a very strident timbre - more square wave than sine!
Si(ne)+(squ)are...
Going even further 'off the wall', if you splice half a sine wave with half a square wave, then that gives a different result. There's a bit more square to this one, and slightly less high frequency 'stuff', but it sounds unusual. There's also lots of DC offset because of the asymmetry in the wave shape.
Gapped sines...
Replacing the square wave cycle with nothing gives a result which sounds nothing like the fragments of sine waves that makes up all of it (plus the nothing!). There are two and a half cycles shown in the example, above: each 'single cycle' is just the sine wave plus a cycle's worth of nothing. The missing sine wave cycles add a lot of harmonics. So is this a single cycle wave, or a three cycle multi cycle with some gaps? The spectrum suggests that it is lots more jagged than it appears...so all of those discontinuities as the sine goes flat obviously mean lots of high frequencies, but we aren't used to discontinuities that hide on the zero axis...
Resonant... 2 cycles in one...
8 cycles in one...
16 cycles in one...
A different approach is to take several cycles of a waveform, and then to give that a very short envelope. In the examples shown, I start with the full size waveform and taper it down to almost zero. This gives sounds which have an intriguing 'resonant' nature to them, and don't forget to try them with sync and FM as well.
When you first see these waveforms, they look like multi cycle waveforms, but the repetition is of the whole of the waveform you see, from the big wave at the start, to the small wave at the end, so it is a single cycle, but it contains multiple cycles.
Chirps
Chirps change the frequency of the cycles within a multi-cycle waveform, and can produce timbres which sound very complex and which can't possibly be coming from a single oscillator playing a tiny fragment of audio (but they are!). In the example above then the frequency doubles over the single cycle. I didn't tweak the ends and so there's a discontinuity when the next cycle starts. This sharp feature in the waveform causes lots of high frequencies, and so this sounds more like a pulse wave than a (mostly) smooth sine-ish waveform.
I know that using multi-cycle waveforms is seen as cheating by some people, and you can find that some oscillators don't have quite the range that they normally do when you need to transpose them a lot (the 16 cycle enveloped 'resonant' waveforms, for example). But I prefer to think of them as single cycle waveforms with unusual frequency content.
One problem which you will encounter very quickly with chirps and some other multi cycle waveforms is tuning. if you thought that tuning FM on analogue subtractive synthesizers was difficult, then the wilder multi cycle waveforms can be even trickier to tune sometimes. I use a guitar tuner pedal to help me tune the oscillator transpose, and the flashing multi-coloured very bright LEDs intended to help guitarists can prove to be a very mysterious distraction to spectators. I'm not sure that there's always enough 'danger' and living on the edge' in many DAWless performances. Pressing buttons on little black boxes isn't very good to watch, but a few guitar tuner pedals can give just a hint of the edgy feel that Keith Emerson used to get with his Moog Modular on stage, or the rotating piano, or...
But how do you make them?
All of this messing about with multi cycle waveforms might have you wondering what esoteric and specialist software tools I use to create them. It isn't actually that unusual - my main tool is Audacity 2.4.2.
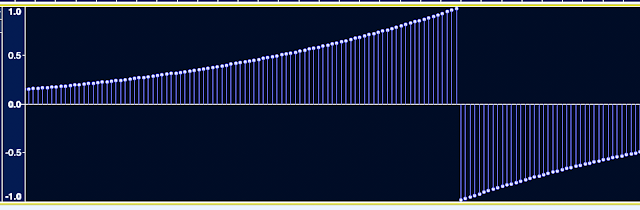
Yes, the free, open source audio editor software that you get free (or they get you to download it) with many domestic 'Transfer your old vinyl albums to MP3s!' devices. Audacity is much better than this use case suggests, and is actually very good zoomed in until you can see the individual samples:
All of the waveforms that you see in this blog post were created using Audacity, and without any fancy plug-ins (although I have written a few plug-ins in Nyquist, which is an 'interesting' programming language!).
Where is the 'End'?
The display of digital samples (from Audacity) shown above has a circle at the top of a vertical line - often called a 'ball and stick' symbol. If you want to exercise your brain then you might like to consider what I said in part 2 about the start and end of a waveform being at the same level....
Let's start by looking at a sampled square wave with only16 samples per cycle. I've shown it as starting with a sample at time zero - the first sample. The last sample of the cycle happens just before the end of the cycle (and the end of the waveform) and is highlighted in light blue. The next sample is the first sample of the next cycle, and is highlighted in orange. The red line highlights the final part of the cycle between the last sample and the first sample of the next cycle.
I would say that the last sample is not at the 'end' of the cycle - it is definitely earlier in time than the 'end' because there is a red line showing the time between the last sample and the start of the next cycle - and the red line is needed to make the period correct (the time between the start and the end). The 'end' of the cycle, for me, is just before the start of the next cycle - which I would say is at the right hand end of the red line. So, for me, the end of the cycle is not the last sample (the blue one), but a tiny bit of time before the first sample of the next cycle - the orange one. And what is the level immediately before the orange sample? Well, it has to to very close to the level of the orange sample. doesn't it? This is what I mean when I say that a waveform begins and ends at the same level. And yes, I'm kind of splitting the first sample into two pieces and saying that it is the start and vanishingly close to the end.
Suppose it was suggested that the zero axis is obviously the start and the end level? (Since the average of the high and low samples is zero) Well, then, the first sample would not be at the start, but would be slightly later. So now the start and the end are somewhere in between the first and last sample - and if you think about it, then the level of 'somewhere between the first and last sample' has to be the same if the start and the end are infinitely close together. So even though the first and last samples are different, the waveform has the same level at the start and the end.
Luckily, you don't need to think about the start or ends of samples in this depth very often!
Audacity 'Single Cycle' Tip Number 1
Audacity makes it very quick and easy to do some tasks that often defeat people - like changing the number of samples in a single cycle waveform. Here's how to do that:
First, select your single cycle in a track. Then go to the 'Effect' drop-down menu. Select 'Change Speed'. (Not any of the other Change options like Pitch or Tempo...).
Then go to the 'New Length' field and type in the number of samples. Don't type in any of the time formats!
Audacity 'Single Cycle' Tip Number 2
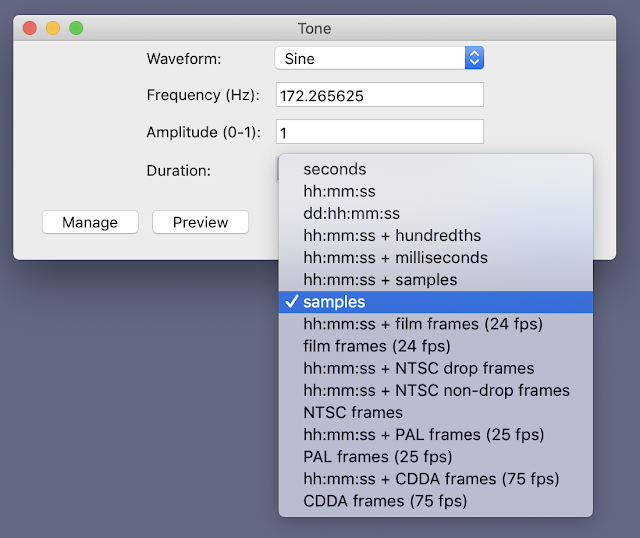
Generating single cycles on wave shapes isn't completely obvious. Here's what you do: Go to the 'Generate' drop-down menu and choose 'Tone'. Enter the frequency (as in table1 above) and the number of samples you want, and press 'OK'
The key to entering samples and not times into those fields is the tiny arrow on the right hand side of the 'Duration' field. When you click on it, you get a drop-down menu that lets you select 'Samples'. This works in the 'Change Speed' dialogue box as well.
Examples
You can download .WAV files of many of the single cycle waveforms in this blog, plus a few more from here. [Not all waveforms are available in every format. I'm not good enough at batching! Think of it as a challenge to find the missing ones and recreate them in the correct format yourself...]
The waveforms were all produced at 44.1 kHz in two sample sizes: 256 and 600, and in three formats: 16 bit, 24 bit and 32 bit float. The user manual for your synthesizer, sampler or drum machine should tell you what format your oscillators prefer.
Next!
In part 4 I will go more into how important spectrums are...
Links
the WAV file format on Wikipedia
Audacity
---
If you find my writing helpful, informative or entertaining, then please consider visiting this link:
 Synthesizerwriter's Store (New 'Modular thinking' designs now available!)
Synthesizerwriter's Store (New 'Modular thinking' designs now available!)
 Buy me a coffee (Encourage me to write more posts like this one!)
Buy me a coffee (Encourage me to write more posts like this one!)