The revisit to 'The 30dB Rule' got me thinking. I realised that there is a lot that most sources don't tell you about waveform displays. Now, if this was a YouTube video, I would be using an eye-catching picture and a bold primary colour headline like:
'Hidden waveform secrets!'
But this is a blog, and I'm not a great fan of the hyper-sensationalism that YouTube seems to encourage. Instead, I've decided to extend 'The 30 dB Rule Revisited' into a few parts, so that I can cover the topic in more detail. (and in even more detail in the next edition (4th) of my 'Sound Synthesis & Sampling' book)
The Waveform
Let's start with the sort of diagram that normally appears in textbooks (or on Pianobook videos!) and build from that.
This diagram shows a single cycle of a sine wave: a 'sine' waveform. The time axis is horizontal, and the amplitude (posh word for volume, size, voltage...) is on the vertical axis. The convention is that you show the positive part first, starting with the first time that the waveform crosses the zero axis, and then the negative part, finishing with the third and final zero crossing. This is just a convention! You could start anywhere on the waveform if you wanted - the waveform doesn't care. But you do need to show at least one cycle, of course.
I normally try to avoid too much maths in this blog, but there's an important formula in the diagram: the relationship between Frequency and the time it takes to complete one whole cycle (this time is called the period, which harks back to pendulums and clocks and physics...). The formula is:
Frequency = 1/Period
Which can be clarified as:
Frequency (in Hertz) = 1/Time to complete One Cycle of the waveform (in ms)
For most audio signals (posh word for sounds, audio voltages...) then the time is usually conveniently measured in milliseconds (thousandths of a second) or microseconds (millionths of a second). Seconds are too big a unit of measurement for the short time that it takes for a sine wave to wobble. For example, a 50Hz mains electricity (in some countries) takes 0.02 seconds to complete one cycle, but it feels much easier to say 20 milliseconds (200ms). In countries where the mains frequency is 60Hz then it takes 16.666... milliseconds (or 0.0166666... seconds) to wobble up and down (or down and up - remember it doesn't matter!)
The formula means that as frequency goes up, then the period (time for one cycle) gets shorter. So a note of 440Hz (an 'A') would have a period of 2.273ms. Up an octave to 880Hz, and the period is 1.136ms. Up another octave to 1760Hz and we have to move to microseconds for expressing the period: 568.2µs or 0.5682ms. This is quite a wobble, if you think about it - the waveform is going from positive to negative in just over half a thousandth of a second.
'Wobbles' is actually a very useful word for describing sine waves. That smooth shape is not an accident - it turns out that if you make a ruler twang, or watch a pendulum swing, or pluck a string, or turn an amp up so that you get feedback from a microphone, then the basic shape of the time wavform that you get is probably a sine wave (or similar). This is because objects in the real world are lazy - they expend as little effort (energy) moving as possible, and the way of something moving back and forth (or up and down, or side-to-side) using the least energy is a sine wave. Look up 'Simple Harmonic Motion' if you want to read about maths and physics... It a bit like: 'the shortest distance between two points is a straight line' - it's one of those fundamental things about how the universe works.
If you want, you can do a totally non-scientific experiment that kind of illustrates this 'least energy' thing. Hold out your arm, with your hand vertical. Now wave it from side to side smoothly counting 'one thousand, two thousand, three thousand...' so that you are doing one cycle every second (a frequency of one cycle per second is 1 Hertz (Hz), and has a period of 1 second!). Then try jerking your hand as quickly as you can between two stationary positions about 100mm apart at the same rate. Instead of a smooth, continuous waving movement, it should be just two brief movements interspersed with waiting. You should find that it feels like you are using much more energy to do the 'Square-shaped' wave than the smooth 'Sine' wave.
So the sine wave is interesting and important because it is least energy and a very smooth shape, and it turns out that it is pretty fundamental in other ways too - you can make any waveshape by adding together sine waves of different frequencies, amplitudes and phases. Phase is just the relationship between two waveforms. If they are 'in phase' (no phase difference) then they go up and down at the same time... Let's look at some diagrams:

Zero crossings are one of the standard places on the waveform that are used to determine phase differences. In the diagram above, the blue circles highlight the zero crossing as the descending sine wave crosses the horizontal zero 'time' axis. From left to right, the two sine wave are: 'In phase', 'slightly out of phase', and 'Out of Phase'. The 'Out of Phase' can also be called 'Anti-phase' - here the two sine waves are opposite: as one goes up, the other goes down, and vice-versa. Phase is normally measured in degrees, as if the time axis was wrapped around a circle. So 'In Phase' is a phase difference of 0 degrees, whilst 'Out of Phase' or 'Anti-Phase' would be 180 degrees. If you keep increasing the phase difference, then eventually you go around and end up at 359 degrees, then 0 degrees as the two waves are in phase again.

The diagram above uses the highest positive peak of the sine wave, which is often easier to see on some waveforms. Again, the three examples are: 'In phase', 'slightly out of phase', and 'Out of Phase'. Phase difference can be measured with any waveform - sine waves are just used here as examples. Waveforms that have lots of similar height peaks, or lots of zero crossings, can be difficult to try and figure out by viewing the waveforms. There are electronic meters which can measure phase in audio signals, and these are used in filter design, loudspeaker crossover design, phase pedal effects, and more. There are filters called 'all phase filters' that only change the phase of signals that pass through them, and a phase meter is used to characterise them.
Earlier, I noted that it was possible to make any waveform by adding together sine waves of different frequencies - well, there's an exception to this... The only wave that can't be made by adding together two or more sine waves is... a sine wave. A sine wave has only one frequency 'inside' it, which is why it sounds so 'pure' when you listen to it, and also it is why it is so smooth in shape. If you added any other sine waves then the shape would be less smooth. Circles and sine waves are the ultimate in smooth!
When you turn down the cutoff of a low-pass filter, then you can hear high frequencies being removed from the signal, and eventually, there is only the sine wave left. So the lowest frequency you hear is the frequency of the sine wave itself, and if you turn the filter cutoff down even lower, then even that sine wave will vanish and you get silence.
Combining and extracting multiple sine waves will be examined in more detail in a future part of this series.
The Waveform - Deeper
Wrapping the time axis around so that it forms a circle is actually a clue to what the 'single cycle' diagram really is - a convenient abstraction that turns reality into something easy to visualise. Actually, a waveform is always moving up and down in time, and the waveform view just captures that up and down movement and makes it visible. If the sine wave is a sound, then the waveform shows how the air is compressed and rarified (not a word we use very much!). If the sine wave is a voltage, then it shows the change of voltage as the sine wave moves up and down. So a waveform is like a long exposure photograph that freezes movement. (or a stroboscope that uses a flashing light to 'freeze' movement...)
Let's dig deeper into a waveform:
The first thing that often surprises people is that the waveform continues both backwards and forwards in time. The waveform repeats over and over again. each time the same. (If the waveform changed over time, then there would not be a single waveform that we could use to represent it.) This means that the start of the waveform (let's start at the first zero crossing) is also the end - remember the wrapping round of the time axis into a circle. This means that the level at the start has to be the same as the end - but it does not mean that the slope of the line at the start has to be the same as at the end.

Above is an example where the level is the same at the start and the end, but the slope is different. In earlier versions of this blog post I said that the slope had to be the same, and this diagram shows that this is not correct. However...
In the diagram above I have moved the discontinuity so that it is more central, and the start and end are now on the zero axis. The slopes at the start and the end are now the same!
It turns out that there is a convention to drawing waveforms that makes them easy to understand. One of the rules in this convention is that you don't have a discontinuity at the start - because it hides the shape of the waveform!
The diagram above shows a triangle waveform displayed in two different ways. One the left is a waveform drawn using the convention, and on the right is the same waveform, but with a discontinuity at the start. As you can see, the waveform on the left is easy to comprehend, whilst the one on the right is more difficult to comprehend. Basically, I'm so used to drawing waveforms that follow the convention that I made an assumption - which is not a good idea!
If there is a discontinuity (the technical word for a sharp change in the waveform) then this will create high frequencies in the spectrum. If you think about what a single sudden change would sound like, then it would be some sort of click. But if that click is caused by a discontinuity in the waveform then it will repeat for every cycle, as so generates lots of high frequencies.
One of the things that is often never explained by most sources is what you can and can't do with a waveform. The levels being the same at the start and the end is the first 'not immediately obvious' thing to note. But the diagram above shows some more.
The steepest slope is one that is almost vertical. It can't be completely vertical, because this would mean that there were several different values at the same time (the horizontal axis is time...), and this isn't usual in this reality. You might like to try thinking about a different universe in which an LFO could have several different values at the same time, and follow it up by Googling '
Schrodinger's Cat'.
You can't have slopes that go over, because this would mean that the waveform was moving backwards in time. Equally, a waveform can't cross over itself, because this would mean that there were two values at the same time.
Finally, you can't have a gap in a waveform - there is always an amplitude value for each time. Now a digital waveform is actually just a series of sample values, but you can't have empty sample values either.
One 'Ah, but...' FAQ at this point often revolves around sawtooth or square waves. They may appear to have gaps in them, but actually it is a very steep (nearly vertical) slope, followed by a much slower slope. On some screens, especially old oscilloscopes, the slow slope is all that is visible, but it doesn't mean there is a gap. In digital samples, a sawtooth can change from a big negative value to a big positive value with a single clock. Some text-book diagrams don't always show sawtooth waveforms as being continuous, and these are called 'idealised' (meaning 'not realistic'). For this post, I'm going to show waveforms in their realistic form, so they will be continuous.
Square waveforms are mostly flat (remember moving your hand from side to side in the experiment, earlier?), but they again have almost vertical slopes joining the two flat portions, and again they are sometimes shown in text-books as idealised pairs of flat output values with gaps between them.
Any time that there is a nearly vertical slope or a sharp corner (like on a square wave or a sawtooth wave), then this indicates that a high frequency is present in the audio (more about this in a future part). If you filter a square wave so that some of the higher frequencies are removed, then you get ripples on the top and bottom portions of the waveform...
These ripples are caused by there not being enough high frequencies to draw in the flat top and the almost vertical edge. In the diagram above, can you imagine what frequency sine wave would be required to cancel out the ripples in the top and bottom portions?
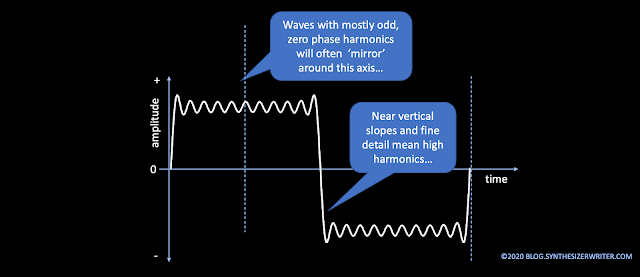
One useful diagnostic technique works well on waveforms which are approximately square. If you imagine a vertical axis in the middle of the flat portion, then if the waveform is 'mirrored' around this axis, then this means that the audio contains mostly odd multiples of the fundamental frequency. If you think about this, then a square wave is the perfect mirror around that mid-flat axis, and it turns out that a square wave does contain only odd multiples of the fundamental frequency.
In physics (and most science) you are often given a theory or Law, and then told when and why it doesn't always apply. In the real world there are often 'ah, but's! So it turns out that the mirroring effect only works when the harmonics are all in-phase... So, phase can sometimes be very important. Let's investigate this:
The above diagram shows the effect of changing the phase of the sine wave that it 3x the fundamental sine wave frequency. 10 degrees (there are 360 degrees when you go all the way round a circle, so 10 degrees is a tiny amount) puts some wobble into the top of the waveform, so it isn't flat any longer. 30 degrees makes the ripple bigger. By the time we get to 60 degrees (cutting a pie into 6 equal pieces gives you six pieces each with a 60 degree angle) then the square wave is almost lost and mostly what we see is a jagged waveform that has a lot of a waveform that is 5x the fundamental sine wave frequency.
So for the shape of a waveform, phase matters. But if you listen to all of these waveforms, then they all sound like a square wave. More on this in a later blog post...
One final thing that you can see just by looking at the shape of a waveform is the 'DC offset'. All of the waveforms so far have been centered on the zero axis, so there's no overall voltage present all the time - the positive and negative bits just cancel out. But the diagram above shows that if the area above that horizontal zero axis line is different to the areas below, then you can get a DC offset. DC offsets can make clipping asymmetric, which changes the sound, and they can cause clicks if you connect a cable carrying an audio signal that has a DC offset.
Just to come full circle, the above diagram also serves as a reminder about 'The 30 or 40dB Rule' - if there is part of the sound that is lower in level by more than about 40dB, then it will be too small to be visible in a waveform. I am pretty sure that this aspect would probably get breathlessly emphasised in some YouTube videos!
Single Cycles
You should now know more about single cycle waveforms, what they are, how they work, and some of the terminology around them. You also now know that the shape of the waveform is related to the timbre (or sound), and that the shape can be produced by adding together different frequency sine waves - although it seems that phase complicates this. But essentially, a single cycle waveform is a little fragment of timbre - actually, it is the smallest fragment you can have that gives a specific sound.
Single cycle waveforms were used in early analogue oscillators, and were chosen to provide a diverse set of timbres. Sine waves for simplicity and 'purity' of tone. Square waves because they sound hollow. Sawtooth waves because they sound sharp and bright. And Pulse waves because they sound thin and buzzy. All of these are fixed 'snapshots' of timbre - they don't change over time.
Over time, oscillators were extended to provide additional waveforms - and significantly, these can change over time: Pulse Width Modulation changes the shape of a pulse wave so that it sounds 'animated' or 'chorussed'. Oscillator sync resets one oscillator waveform using another, and so generates a distinctive, glitchy sound.
Using wavetables instead of fixed singe cycle waveforms allows the timbre to be changed over time: either smoothly by interpolating from one waveform to the next, or simply jumping abruptly from one to the next, which can give a fascinating 'glassy' texture. The ultimate smooth and long wavetable is a sample, of course, with a long looped sustain and a long looped release.
So there's a basic split between the single cycle, 'fixed' waveforms, and the multi-cycle, 'timbre changes with time' waveshapes (made from wavetables or samples). Of course, the ultimate 'timbre changes over time' is noise, where it is randomly different every time.
There's a simple model for sound synthesis that has Controllers controlling sound Sources like oscillators whose outputs are then altered in timbre and volume by Modifiers to produce the final sound output. When the output of an oscillator can change timbre over time then it stops being a pure 'Source' of sound of acquires some of the functionality of a Modifier, but then models are only supposed to be approximations of reality.
The table above fills in some of the possible sound Sources and sound Modifiers. One common application of the Source and Modifier model is for subtractive synthesis:
The above diagram shows how the oscillators and noise are treated as Sources, but it also has PWM (Pulse Width Modulation), Oscillator Sync, and FM as sources. The mixer is also interesting - does changing the mix between Sources count as a Modifier?
The diagram above extends the 'Modifiers' section so that it includes PWM, Sync and FM. This effectively leaves the oscillators with only fixed single cycle waveforms as Sources, plus noise.
Here's a table which emphasises that the only non-Modifier sound Sources that don't 'change timbre over time' are single cycle oscillators and noise generators.
Simple oscillators with just a few single cycle waveforms (plus noise generators) are the main source of sound in synthesizers, but so far the only waveshapes that have been mentioned here are sine, square, sawtooth and pulse. This might appear to be a major limitation, and so the only area worth looking at might seems to be the Modifiers... But it turns out that this is not the case at all, and the next blog post will examine what you can do to exploit the possibilities of single cycle waveforms as much as possible.
Analogue and Digital
I'm adding a quick note here because I didn't explicitly state that everything above applies to both analogue and digital synthesizers. The '30dB Rule' probably applies more to 'old-school' analogue oscilloscopes where the bright lines are a bit fuzzy, whilst the revised '40dB Rule' is more applicable to modern LCD displays which have less fuzziness.
Links
Pianobook videos (This one describes an ADSR envelope...)
Pianobook.co.uk (Free user-created samples (crowd-sourced samples?))
Schrodinger's Cat (A sideways route into quantum physics...)
---
If you find my writing helpful, informative or entertaining, then please consider visiting this link:
 Synthesizerwriter's Store (New 'Modular thinking' designs now available!)
Synthesizerwriter's Store (New 'Modular thinking' designs now available!)

























No comments:
Post a Comment