The 30 dB Rule Revisited - [Single Cycle part 1]

Technology changes all the time, sometimes for the better. One of the background tasks that tends to get forgotten is to revisit and re-assess old assumptions, and to update them when necessary. The mains electricity wiring in a house is one example - the insulation in cables does not last forever, and rubber, PVC and plastics all degrade over time. Recently, I have been blowing the dust off some of my archives of audio samples, and it reminded me of one of the first articles that I wrote for Sound On Sound magazine... It is still available on the Interweb:

SOS - The 30dB Rule   

It set me thinking: how has time changed this 'rule of thumb' that says that if you look at a waveform, you can only see the 'top' 30dB of whatever is in it? I was curious to see if advances in technology meant that this needed a revision...

Into the past...

May 1986 is over 35 years ago, and a lot of the things that you now probably use everyday didn't exist in anything like their current form: the World Wide Web, the Internet, HTML, cheap domestic microwave ovens, cheap laptop computers, LCD video monitors, mobile phones, MP3, DAT, DVDs, DAWs... and high streets full of little more than charity shops and coffee shops. 

Digital audio was possible, in a limited way, on a hobbyist computer. If you were in the know, then researchers in places like George Lucas's Sprocket Systems were working on prototype DAW-like technology, and if you had lots of money, then New England Digital's Synclavier was shipping direct-to-disc recording of digital audio, or you could sample at 8-bit resolution on a Fairlight CMI Series II, whilst you saved up for the recently-released Series III with 16-bits! Most ordinary hi-tech musicians were limited to just using computers for simple audio file editing, or for another relatively new innovation: MIDI. 

So, my samples from this time were mostly 8-bit, sampled at 8, 16, or maybe even the insanely high rate of 32kHz! They were mostly kept on 3.5 inch floppy disks (From Sony, which were encased in plastic and so weren't actually 'floppy' at all...) or on a hard drive which would be a few hundred Megabytes in a case about twice the size of a modern hard drive with a few Terabytes. To look at the files, CRT (Cathode Ray Tube) monitors would be used - VGA resolution (640x480) monochrome LCDs didn't appear until 1988, and colour LCDs didn't become affordable until the 1990s. You might like to create a graphic image sized 640 x 480 pixels on your current computer to see just how small it really is - on my 27 inch 5K (5120 x 2880 pixels) monitor it covers about the same area as a credit card.

So here's an 8bit sine wave, displayed more or less 1:1, so there are 256 pixels from the highest to lowest peak (except it isn't - no matter what I do, my browsers won't show the graphic actual size. Strange...). Anyway, just imagine that the following graphic image is 256 pixels in height: 

Now on a VGA monitor, that 256 pixel high sine wave is going to be taking up just over half of the screen height, so it is going to be pretty large. If you looked at the same sine wave on an Oscilloscope (You can still get them, although now they are digital, have LCD screens, don't get hot, and weight very little!) then you would probably set the controls so that it occupied about the same sort of percentage of the screen height - especially since 'scopes often have all sports of readout on the screen for frequency, voltage, range, offset... Notice that despite the 8-bits and the small image, it looks like a sine wave!

To 2020...

If we now do this with 16 bits and a bigger screen, then we can fast forward to 2020. We can take the normalised output as our maximum output level (let's call it 0dB), then we can compare it with a higher frequency (4x freq) sine wave attenuated by 30dB (i.e at -30dB). Because these are going to show relative levels, I'm not going to align the bits to pixels here, especially because I can't show 16 bits on a sensibly-sized screen (the screen would have to be 65,536 pixels high, which is more than 20x the vertical resolution of my current screen (2880 pixels).

So, from left to right, we have the sine wave at 0dB, a 4x frequency sine wave at -30 dB, and the result of mixing them together. The waveform on the right looks distorted, and is obviously not a sine wave, and if you listen to it, then it is very easy to hear the 4x frequency sine wave because it is only 30dB down, and your ears are good over a much bigger dynamic range than that. 

But the middle screenshot is particularly interesting. A signal 30dB down is just about visible on modern screens, but you can imagine that if this was an oscilloscope with a slightly fuzzy line of light as the display, then it might be possible to see the sine wave. But many 2020 synthesizers feature waveforms shown on small OLED displays that are not even 256 pixels high, and so the vertical resolution is worse than a VGA monitor, and worse than the 8-bit example shown above.

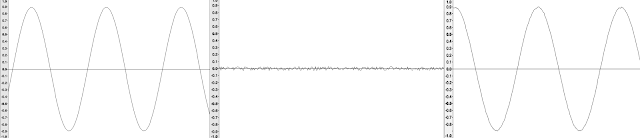
So let's try the same process at -40dB.

As before, from left to right we have the sine wave at 0dB, then the 4x frequency sine wave at -40dB, and then the result of mixing them together. The middle screenshot is now much smaller, and the sine wave on the right looks like...a sine wave. If you listen to it, then you can hear the 4x sine wave. but it is not obvious from looking at the screenshot that the sine wave is impure at all.

Finally, how about adding noise instead?

This time the middle screenshot is noise at -40dB. The right screenshot is the result of mixing the sine wave and the noise. It looks pretty much like a sine wave to my eyes, although when you listen to it, you can hear the added noise (it is only 40dB down). On an oscilloscope, the width of the line is going to hide the noise even more effectively.

Let's simulate that:

So anything smaller - like below -40dB - is not going to be visible to your eyes at all...

The 40dB Rule...

Over 30 years of progress has given us better displays, and cheaper, lighter oscilloscopes. But it seems that just 'looking' at waveforms still only tells you about the top 40dB or so of the signal. Anything lower than that is not going to be visible. 

"You can only see the top 40dB or so of a waveform..."

and a useful pair of corollaries:

"Your ears are much better at hearing than your eyes. Don't trust waveforms."

"On a small OLED screen, you may only see the top 30dB of a waveform, or less."

At one time, it was quite popular for synthesizer manufacturers to provide the ability to draw waveforms (usually using light pens, but these days you would probably do it with a mouse)... Hopefully, you now know why this is not a good idea if you want to have control over anything other than the very loudest component parts of the sound.

Only today, I saw a Facebook post where a person was describing how an analogue synthesizer software emulation VST had been prepared with great care, emphasising that the actual and emulated waveforms had been compared on an oscilloscope 'very carefully'. Unfortunately, you now also know that this is not a good technique to base comparisons on. Instead, spectrum analysis of the waveform would show the frequencies that were present down to levels much, much lower than -40dB!  

---

If you find my writing helpful, informative or entertaining, then please consider visiting this link:

Buy me a coffee

Synthesizerwriter's Store (New 'Modular thinking' designs now available!)