Should I look at the Spectrum, or the Waveform? - [Single Cycle Part 4]

One of the 'useful things to remember' that I have always had in my mind is something that I learned reading through a pile of old 'Wireless World' magazines from a cupboard at the back of the Physics Lab at my school:

Spectra can be better diagnostics than waveforms 

(I'm using 'Spectra' here as the plural for 'Spectrum'. You can replace it with 'Spectrums' if you prefer... I won't tell anyone.)

It was from an article where they described how a project to recreate the sound of a church organ by reproducing the waveform failed because the result sounded totally different. From the first part of this series then you may not be suspecting that they probably only matched up the 'top' 30 to 40 dB of the sound (the visible bit on a 'scope) - the '30 dB Rule' as I call it. When I've experimented with A/S (Analysis/Synthesis), the iterative synthesis technique where you analyse the target sound/timbre, get a reasonably close synthesised version of it, then subtract the two to get a 'residual', and then synthesize that, and so on, then I wondered if you could use this to keep removing layers of 40 dB or so of visibility, getting a better approximation each time...

Anyway, a reasonably good spectrum analyser is going to show you a lot about the spectrum of a sound - and the harmonics that it shows will give you detail well below 40 dB down. But the spectrum isn't perfect either, because it shows the magnitude of the harmonics in a sound, but generally, not the phase relationships. As was shown in part two of this series (Single Cycle 2), then phase relates to the tiny timing difference between the same point on two waveforms - it could be zero crossings, or positive peaks: anywhere that is easy to compare. Although the horizontal axis is the 'time' axis, many people think of the phase more in terms of the shape of the waveform 'sliding' horizontally - which kind of removes the link that is implicit in a 'time waveform'! But this 'sliding' approach does explain how it is possible to have phase differences that are not directly related to time - if you take a waveform and invert it, the two waveforms are then 'out of phase' even though neither of them has moved in time (although it might take a finite amount of time for the inversion to happen, of course!)

Where this gets interesting is when the waveform is not symmetric. If you invert a sawtooth, then what does 'phase' mean? The zero crossing position gives a reasonably neat alignment of the sawtooth waves, but using the positive peak is confusing, and it would be better to use the fast 'edge' between the positive and negative peaks - but is this then ignoring the time for that fast edge. So should the zero crossing in the middle of the fast edge be used? 

When the waveform is even less symmetric, then neither peaks nor zero crossings may be a viable choice for a reference point. In the example above, inverting the waveform means that the positive peaks are different, and there are two candidate zero crossings. When waveforms are this different, then phase starts to lose any meaning or value for me... Of course, you could use the fundamental of the two waveforms, in which case the inverted waveform would be seen as out-of-phase or inverted.

Phase is important in filter design (like in loudspeaker crossovers, for example), in noise cancellation (two anti-phase signals will cancel out to give silence, although getting two precisely out-of-phase signals is not very easy in a large volume in the real world), and in creating waveforms (in additive synthesis, for example). It turns out that the phase can be very important as a diagnostic tool: so a visually smooth filter cut-off might well be hiding a phase response that goes all over the place. 

Why is Phase Important?

The standard example to show why 'phase is important' is to take a 'square'-ish waveform made from a few odd harmonics, and to change the phase of one of them. Suddenly the square wave isn't square any longer... 

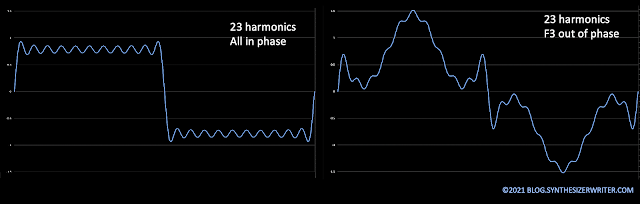
What has always fascinated me is the number of harmonics that are required to get waveforms that are close to the mathematically perfect, sharp, linear wave shapes that you see in text books. In the example above, then 23 harmonics are used to make a 'wobbly' square wave - actually, of course, then because a square wave is made up of odd harmonics, then there are not 23 actual sine waves used to make up the square wave, since just under half of them have zero amplitude. 

So when the phase of the third harmonic (three times the frequency of the fundamental) changes, then two things happen. Most text books will show the changed waveform, and will note that it still sounds like a square wave (the harmonics are the same...). But it is more unusual for there to be any mention of the change in the peak amplitude - the 'F3 out of phase' waveform on the right hand side is about 50% bigger, peak-to-peak, than the 'conventional' square wave approximation on the left hand side. It turns out that changes in the phase of harmonics can affect the shape and the peak-to-peak amplitude, and more: the phase of the harmonics can be used to optimise a waveshape for some types of processing, although this is normally used in applications like high power, high voltage electricity distribution rather than audio.

But this 'phase is important to the shape of the waveform' principle applies to any waveform, and this can give surprising results. Take a triangle wave: it has only odd harmonics, and they drop off rapidly with increasing frequency, so the triangle really is what it sounds like: a sine wave with a few harmonics on top. Now you are probably intrigued by this, and rady to explore it yourself, so there's a very useful online resource at: http://www.mjtruiz.com/ped/fourier/ It is an additive synthesizer that lets you explore the amplitude (volume/size/value) of harmonics, as well as their phase! (This is called a Fourier Synthesizer, after the Fourier series, which is the mathematics behind adding different sine waves together to give waveforms...)

Here's a screenshot of a triangle wave produced using the Fourier Synthesizer from M J Ruiz:

I have edited the colours of the sliders to emphasize the harmonics which have zero amplitude (black), the harmonics which are 'in phase' with the fundamental (blue), and the harmonics which are 'out of phase' with the fundamental (orange). In-phase is shown as a value of 0 in the screenshot - meaning zero degrees of phase, where a complete cycle would be 360 degrees. Out-of-phase is shown as 180 degrees - half way round a cycle of 360 degrees.

 The screenshot above shows an unedited view of the same triangle wave, but with the phases changed so that all of the harmonics are in-phase. The result is more like a slightly altered sine wave than a triangle wave - but it sounds like a triangle wave...

Earlier I pointed out that the sound of a square wave with the third harmonic changed in phase was the same as a square wave with no phase change on the third harmonic. It turns out that your ears are not sensitive to phase relationships of this type, and so the square waves, and the triangle waves, all sound the same regardless of the phase relationships of the harmonics. BUT if you change the phase of a harmonic in real-time, then your ear  WILL hear it. Static phase relationships between harmonics are not heard, but changes in phase are...

If you think about it, then this is not as surprising as it might at first sound. Your ears are very good at detecting changes of phase, because that's how they know what frequency they are hearing! But fixed differences in phase just change the shape, and your ears don't pick that up. One possible explanation for this is that your ears evolved as they did because the harmonic content of sounds was important for survival (maybe locating sources of food, or danger!), but the shape of the waveform was not. Discovering that the human hearing system is not optimised for sound synthesis may be a disappointment for some readers...

One other thing that you may have noticed in the Fourier Synthesizer screen-shots is the small amplitudes of the harmonics for the triangle wave. The sliders used to control the amplitudes are linear, whereas the way that harmonics are typically shown in a spectrum analyser is on a log scale: as dBs. 

The spectrum above shows this quite nicely (plus some other interesting things as well, most of which are because this isn't a 'real' triangle wave, but one that I constructed inside Audacity). The fundamental frequency of the waveform is 50Hz and goes higher than the 0dB reference level (maybe +5dB), and the 3rd harmonic at 150 Hz is at about -24 dB which translates to -19 dB when you add that +5dB. But the Fourier Synthesizer showed this as 0.11 on the linear scale. It turns out that -19dB is a voltage ratio of about 0.11. Thhe 5th harmonic is at -33dB, which is -28dB when you add the +5 dB, and this is a voltage ratio of 0.04, which matches the Fourier Synthesizer value of 0.04. The 7th harmonic is -41dB, which becomes -36 dB which is  0.016, and the Fourier Synthesizer has 0.02. 

So the spectrum analyser harmonic levels are nice numbers, whereas the Fourier Synthesizer harmonics amplitudes are small numbers. I much prefer the spectrum analyser log scale, and here's a chart that shows how the spectrum analyser dBs down relates to the Fourier Synthesizer slider value:

Note that 0.5, which means that you set the Fourier Synthesizer slider to the half way point, corresponds to -6dB. Anything below -40dB is a slider value of below 0.01, which means moving that slider by 1 hundredth of its travel, which is a small distance. This table kind of reinforces why the 40dB Rule mentioned in part 1 of this series exists - the slider values are just tiny, and this means that the harmoncs are going to be tiny too. Probably too small to be seen on a screen!

So if I was going to be designing a Fourier Synthesizer, or an Additive Synthesizer, then I wouldn't use the slider values, because they are typically small and are going to be hard to set easily. Instead I would use the dB values, which are simple numbers and are going to be much easier to set correctly.

Conclusions (so far)

From this series so far, there's quite a lot of things that we now know about waveforms and spectrums:

- Anything below -40dB is going to be difficult to see on a screen

- A single cycle waveform might have unusual harmonics in it

- The waveform does not always tell you what harmonics are present

- The spectrum always tells you what harmonics are present

- Spectra can be better diagnostics than waveforms 

- Phase is important for waveshapes, but not what they sound like

- Your ears can only hear changes of phase

- Controlling the level of harmonics should use a log (dB) scale

In the next part, I'm going to talk about noise in single cycle waveforms, and why it doesn't do what you might expect.

---

If you find my writing helpful, informative or entertaining, then please consider visiting this link:

Buy me a coffee (Encourage me to write more posts like this one!)

Synthesizerwriter's Store (New 'Modular thinking' designs now available!)